MATEMATIKA
Borka Marinković
Poligonalni brojevi
Isključiva sledstvenost

Pitagora |
„Algebra je pisana geometrija, a geometrija je algebra u slikama”, jednostavno je objasnila vezu između algebre i geometrije čuvena francuska matematičarka Marija-Sofija Žermen.
NOVOGODIŠNJE MATEMATIČKE ČESTITKE |
23 +33 +43 +53 +63 +73 +83 +93=2024
(22*23*24) / 6 = 2024
(2023 2 -1) / 2022 = 2024
2024 je poligonalni, preciznije: tetraedarski broj. |
Poligonalni ili, po nekim matematičarima, figurativni broj je prirodan broj predstavljen tačakama (kružićima), raspoređenim u obliku pravilnog poligona (geometrijska figura koja ima jednake sve stranice i sve unutrašnje uglove), pri čemu su tačke jedinice. Poligoni se grade tako što se, od obeležene početne tačke, grade stranice povećavanjem broja tačaka, a zatim se dodaju potrebne dodatne tačke između njih kako bi se formirao poligon.
Eukrit, učenik antičkog filozofa Filolaja, pripadnika Pitagorejske škole, brojeve je predstavljao slaganjem kamenčića tako što je jedan kamenčić označavao jedinicu, dva dvojku itd. Oblikovanjem kamenčića u geometrijske likove, Pitagorejci su povezali aritmetiku i geometriju.
1, 1+2, 1+2+3, 1+2+3+4… Ili: 1, 1+3, 1+3+5, 1+3+5+7…
Za Pitagoru je sve bilo broj, a 10 je bio najlepši broj jer se dobija sabiranjem prva 4 prirodna broja (1+2+3+4=10).
Iz istorijskih izvora je poznato da su se Pitagorejci molili nad brojem 10, izgovarajući: „Blagoslovi nas, o Božanski broju, koji si stvorio i bogove i ljude. O sveti, sveti Tetraktise! U tebi je vrelo i u tebi su koreni prirode koja večno cveta.”
Aritmetika preko dosadašnjih granica
Starogrčki matematičar i astronom Hipsikle je došao do prve opšte definicije pojma k-ugaonog broja (k=3,4,5,6…) koju je citirao Diofant u svom delu „Poligonalni brojevi”: „Ako postoji mnogo brojeva počevši od 1 i ako ih povećavamo za istu razliku, tada je, ako je uzastopna razlika 1 zbir svih brojeva, trougaoni broj; ako je razlika 2 kvadratni broj, kada je 3 petougaoni…”

Pjer Ferma |
Francuski matematičar Pjer Ferma se bavio proučavanjem poligonalnih brojeva. Dotadašnji rad matematičara na poligonalnim brojevima komentarisao je u pismu Mersenu i Paskalu: „Ja sam bio prvi koji je otkrio vrlo lepu i opštu teoremu da je svaki broj ili trougaoni ili suma 2 ili 3 trougaona broja; svaki broj je kvadratni ili suma 2, 3 ili 4 kvadratna broja; petougaoni, ili suma 2, 3, 4 ili 5 petougaonih brojeva; analogno za šestougaone, sedmougaone i sve ostale poligonalne brojeve. Ne mogu da dam dokaz koji zavisi od dubokih i teško razumljivih osobina brojeva; nameravam da tome posvetim celu knjigu i ovaj deo aritmetike unapredim preko dosadašnjih granica.”
Takva knjiga nije nikada objavljena! Tek je matematičar Koši dao prvi dokaz Fermaove teoreme, čime je utemeljen doprinos razvoju savremene matematike. Ojler se takođe interesovao za ove brojeve. Njegova je formula za trougaone brojeve. Po dogovoru, 1 je prvi poligonalni broj za bilo koji broj strana poligona.
Zbir dva trougaona broja je kvadratni broj!
Najčešći i osnovni tipovi poligonalnih brojeva su trougaoni i kvadratni, a poligonalni brojevi se mogu formirati za bilo koji broj stranica pravilnog mnogougla. Trougaoni broj se dobija kada se početnoj tački u sledećem redu dodaju 2 tačke, čime se formira jednakostranični trougao. Broj 6 se dobija dodavanjem nove tačke u sledećem redu, pri čimu tačke i dalje obrazuju jednakostranični trougao. Još veći jednakostranični trougao od 10 tačaka dobija se dodavanjem još jedne tačke u sledećem redu, itd.
Pitagori se pripisuje otkriće da je zbir prvih n prirodnih brojeva trougaoni broj:
1+2+3+…+n=1/2 n(n+1)
Trougaoni brojevi su: 1, 3, 6, 10, 15, 21, 28, 36…105… A zbir dva uzastopna trougaona broja je kvadratni broj.
Kvadratni brojevi se formiraju po istom principu kao trougaoni, ali se dodavanjem tačaka gradi kvadrat. Drugi kvadratni broj dobija se sabiranjem prva dva neparna broja 1+3=4, treći sabiranjem prva 3 neparna broja 1+3+5=9, četvrti sabiranjem prva 4 neparna broja 1+3+5+7=16, itd. Uopštavajući, to je formula
1+3+5+…+(2n-1)=n2
Kvadratni brojevi su: 1, 4, 9, 16, 25, 36, 49…100…
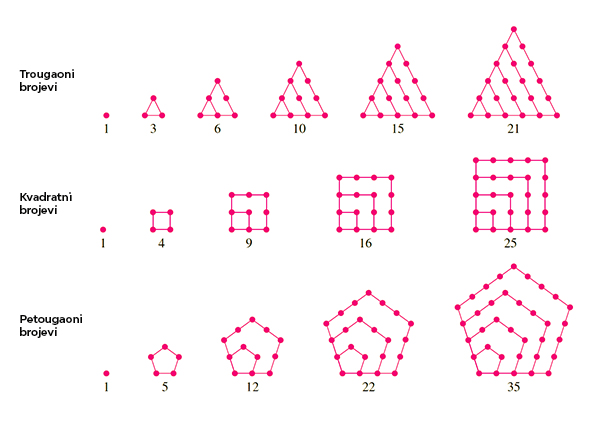
Umesto tačkica i krugova
Centralni poligonalni brojevi takođe mogu biti trougaoni, kvadratni, petougaoni itd. Ovi brojevi se formiraju tako što se oko jedne centralne tačke gradi pravilan poligon. Svaki idući pravilan poligon od m stranica ima za m više tačaka od prethodnog jer se svakoj stranici dodaje jedna tačka.
Centralni trougaoni brojevi su: 1, 4, 10, 19, 31… a mogu se izračunati po formuli: 1/2(3n2-3n+2). Centralni kvadratni brojevi su: 1, 5, 13, 25, 41… a formula glasi: 2n2-2n+1. Takođe, postoje petougaoni (pentagonalni), šestougaoni (heksagonalni) i naredni centralni poligonalni brojevi.
| ZADATAK ALBERTA ANŠTAJNA |
|
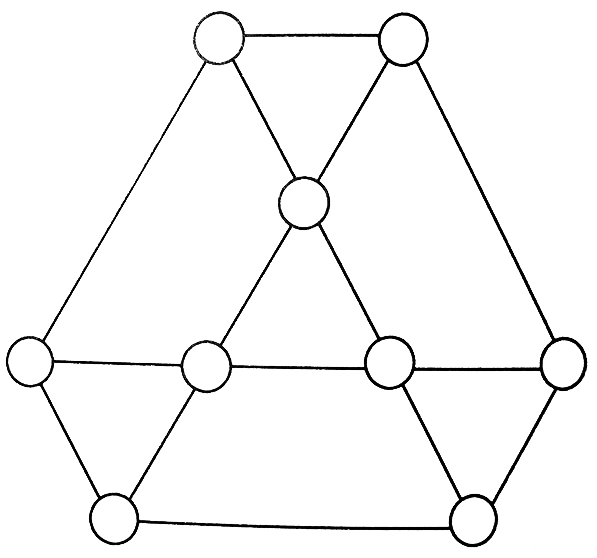
U prazne krugove upisati brojeve od 1 do 9, tako da je u svakom krugu jedan broj, pri čemu su zbirovi brojeva u temenima svakog od 7 jednakostraničnih trouglova međusobno jednaki. Zadatak ima više rešenja, a može se dokazati da je zbir brojeva u svakom trouglu 15. |
|
Iznosi binomnih koeficijenata
Piramidalni ili kvadratni piramidalni broj je figurativan broj formiran od sfera (umesto tačkica-krugova) u obliku piramide čija je osnova kvadrat. Kvadratni piramidalni brojevi mogu biti izraženi kao sume binomnih koeficijenata.
Binomni koeficijenti su tetraedarski brojevi. Ova formula izražava kvadratni piramidalni broj kao zbir dva tetraedarska broja na isti način kao što su kvadratni brojevi sume dva uzastopna trougaona broja. Kvadratni piramidalni brojevi su povezani sa tetraedarskim brojevima.
Binomna teorema je jedna od osnovnih teorema algebre i određuje koeficijente binoma (dvočlani algebarski izraz) predstavljen u razvijenoj formi. Po ovoj teoremi, moguće je predstaviti stepen binoma (x+y)n kao zbir sabiraka oblika k*xayb, gde su k koeficijenti pozitivni celi brojevi i pri čemu je zbir eksponenata a i b jednak n za svaki sabirak (a+b=n).
Koeficijenti u binomnom razvoju nazivaju se binomni koeficijenti i oni su identični brojevima koji se pojavljuju u Paskalovom trouglu. Isti ovi koeficijenti se javljaju u kombinatorici gde je xn-kyk jednak broju različitih kombinacija k elemenata koji se biraju iz skupa od n elemenata.
Prirodni brojevi kao što su savršeni brojevi - Mersenovi, Fermaovi, Fibonačijevi, Lukasovi… - povezani su sa poligonalnim brojevima.
ZADATAK JANGA HUIJA
(1238-1298) |
ZADATAK STANKA
PRVANOVIĆA (1904-1982) |
ZADATAK HENRIJA ERNESTA
DJUDENIJA (1857-1930) |
Rasporediti brojeve od 1 do 33 u kružiće sa slike, tako da zbirovi brojeva na svakom od 4 kruga i svakom od 4 prečnika budu isti.
(Rešenje: U centru je 9, u najmanjem krugu, počevši od najvišeg polja u smeru kazaljke na satu: 10, 22, 7, 30, 2, 18, 25, 24. U sledećem krugu: 23, 13, 19, 14, 29, 26, 11, 3, u narednom krugu: 16, 1, 31, 21, 32, 17, 5, 15), u najvećem krugu: 20, 33, 12, 4, 6, 8, 28, 27). |
Na datoj figuri su označene neke karakteristične tačke.
1. Može li se ta figura nacrtati jednim potezom?
2. Ako može, iz kojih tačaka se može krenuti? (2, 6) |
Popuniti peostala polja na slici tako da zbir kvadrata brojeva u dva susedna polja bude jednak zbiru kvadrata brojeva koji su povezani linijama. Brojevi moraju biti različiti.
(Rešenje: 16, 2, 49, 22, 19, 8, 14, 47, 26, 13) |

|
Borka Marinković
.
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|

